线性代数笔记
目录:
- 行列式
- 向量
- 矩阵
行列式
定义
给定一个n阶方阵 $A$,定义 $A$ 的行列式 $det(A)=|A|$,是一个数。
几何意义:表示长度、面积、体积。
当 $n=1$ 时,即 $det(a)=|a|$,$a$ 为一位坐标上的有向长度。
可以理解为一个函数:
$$M_n(R)→R
A→|A|=det(A)$$
基本构成
$$
\left|
\begin{array}{cccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array}
\right|
$$
$a_{ij}$ 表示第$i$行(row),第$j$列(col)的元素(或称元)
二阶线性方程组与二阶行列式
$$\begin{cases}a_{11}x+a_{12}x=b_1 \\a_{21}x+a_{22}x=b_2\end{cases}→\begin{cases}x_1=\frac{b_1a_{22}-a_{12}b_2}{a_{11}a_{22}-a_{12}a_{21}} \\x_1=\frac{b_2a_{11}-a_{21}b_1}{a_{11}a_{22}-a_{12}a_{21}}\end{cases}$$
记
分母$D$=$\left|\begin{array}{cc}a_{11}&a_{12}\\a_{21} & a_{22}\end{array}\right|$,称$D$为系数行列式
可将$x_1,x_2$的分子分别写成
$$D_1=\left|\begin{array}{cc}b_1 & a_{12}\\b_2 & a_{22}\end{array}\right|和 D_2=\left|\begin{array}{cc}a_{11}&b_1 \\a_{22} & b_2\end{array}\right|$$
可得
$$x_1=\frac{D_1}{D},x_2=\frac{D_2}{D}$$
二阶行列式的几何意义
$$det\left|\begin{array}{c}a&b\\c&d\end{array}\right|=平行四边形“S”的面积=\pm||α||\times||β||\times sin\theta$$
其中$α=\left|\begin{array}{c}a\\c\end{array}\right|,β=\left|\begin{array}{c}b\\d\end{array}\right|$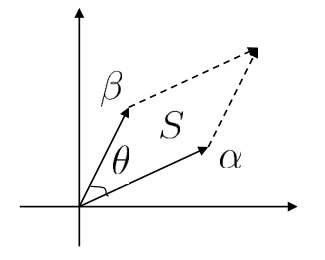
二、三阶行列式计算方法
$$det(A)=主对角线元素之积-副对角线元素之积$$
全排列和对换
排列
将n个不同的元素排成一列,叫做这n个元素的全排列
逆序
元素先后次序与标准次序(通常为从小到大)不一样时,称构成一个逆序
逆序数
若标准次序为从小到大,则 $p_1p_2···p_n$ 的逆序数为 $p_i$ 后比 $p_i$ 小的个数 $t_i$ 的总和 $\sum_{i=1}^n t_i$
逆序数为奇数为奇排列,逆序数为偶数为偶排列
对换
对换包括相邻对换和对换
任意(相邻)对换排列中的两个元素,排列改变奇偶性
奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数为偶数
行列式性质
1.行列式与转置行列式相等 $det(A)=det(A^T)$
2.对换行列式的两行(列),行列式变号
$$det(α_1,α_2,···,α_i,α_j,···α_n)=-det(α_1,α_2,···,α_j,α_i,···α_n)$$
3.若有一行(列)全为0,行列式为0
4.若有两行(列)完全相同,行列式为0
$$det(α_1,α_1,···,α_n)=0$$
5.若有$k$为一行(列)公倍数,$k$可提出在行列式外面(逆运算也成立)
$$det(α_1,α_2,···,kα_i,···α_n)\overset{r_i/k}{=}k·det(α_1,α_2,···,α_i,···α_n)$$
6.若有两行(列)成比例,行列式为0
7.若某一行(列)元素都为两个数之和,则可将行列式拆分为两个(其余元素不变)
$$det(α_1+α_2,···,α_n)=det(α_1,···,α_n)+det(α_2,···,α_n)$$
8.将某行(列)各项乘同一个数后加到另一行中,行列式不变
$$det(α_1,α_2,···,α_i,···α_n)\overset{r_i+kr_j}{=}det(α_1,α_2,···,α_i+ka_j,···α_n),(i\neq j)$$
初等变换
行列式有三种初等变换,对应上述性质
1.行交换
2.行乘法
3.行加法
行列式的计算
行列式计算公式
通过拆分每列每行只保留一项,正负号与置换阵(排列数)有关
$$n阶行列式=\sum_{j_1j_2···j_n} (-1)^t a_{1j_1}a_{2j_2} ···a_{nj_n}$$
其中$j_1j_2···j_n$为排列数,$t$为排列式奇偶性
一般转化为上(下)三角行列式计算
$$三角行列式
=a_{11}a_{22}···a_{nn}(主对角线)\\
=(-1)^\frac{n(n-1)}{2}a_{n1}a_{(n-1)2}···a_{1n}(副对角对角线)
$$
降阶
将A的行(列)消去,写成n-1阶行列式的组合,进行递归运算
余子式
设 $A=|{a_{ij}}|_ {n\times n},M_{ij}为A划去第i行第j列的n-1阶矩阵$
$detM_{ij}$称为余子式
$c_{ij}=(-1)^{i+j}detM_{ij}$称为代数余子式
行列式展开定理
有较多0的情况或者可化0的时候使用,一般将某行(列)化为只含1项非零项。
$\det A=a_ {i1}C_ {i1}+a_{i2}C_{i2}+\cdots+a_{in}C_{in},\forall i,j=1,\cdots,n$
如果某一行中有很多0,可以减少计算代数余子式。
典例:范德蒙(Vandermonde )行列式
$$
D_{n}=\left|\begin{array}{ccccc}
1 & 1 & 1 & \cdots & 1 \
x_{1} & x_{2} & x_{3} & \cdots & x_{n} \
x_{1}^{2} & x_{2}^{2} & x_{3}^{2} & \cdots & x_{n}^{2} \
\vdots & \vdots & \vdots & \ddots & \vdots \
x_{1}^{n-1} & x_{2}^{n-1} & x_{3}^{n-1} & \cdots & x_{n}^{n-1}
\end{array}\right|=\prod_{1 \leq i<j \leq n}\left(x_{j}-x_{i}\right)
$$
向量
n维空间中的点
定义$n$维空间的点为一个$n$元的有序数组$x=(x_1,x_2,···,x_n)$
点的相等
$$
x_i=y_i,\forall 1\leq i \leq n
$$
若每一项相等,则称$x=(x_1,···,x_n)$与$y=(y_1,···,y_n)$相等
点的和
$$
x+y=(x_1+y_1,···,x_n+y_n)
$$
满足:
1.交换律:$x+y=y+x$
2.结合律:$(x+y)+z=x+(y+z)$
3.存在零元:x+0=x
4.存在负元:x+(-1)x=0
数乘
$$cx=(cx_1,···,cx_n)$$
向量的定义
向量指空间中具有一定长度和方向的有向线段,通常记起点为$A$,终点为$B$的向量为$\vec{AB}$或$\pmb{AB}$
如果固定向量的期间为远点,则向量等同于n维空间中的点、n元有序数组
记为:$\pmb{a}=\begin{pmatrix}
a_1\\
\vdots \\
a_n\\
\end{pmatrix}或=(a_1,···,a_n)$
向量的加法(减法)
满足三角形法则,满足结合律,交换律,结合律,存在零向量,存在负向量
$$\pmb{a+b}=\begin{pmatrix}
a_1+b_1\\
\vdots \\
a_n+b_n\\
\end{pmatrix}$$
向量的数乘
长度$\times n$倍,方向不变
向量的线性组合
设$\pmb{V_1},\pmb{V_2},···,\pmb{V_m}$为$m$个$n$维向量,称$c_1\pmb{V_1}+···+c_m\pmb{V_m}$为向量$\pmb{V_1},\pmb{V_2},···,\pmb{V_m}$的线性组合
在三维空间中,几个向量的所有的线性组合通常为一条直线、一个平面或一个3维空间,特殊为点(均为零向量)
向量的点积
设$\pmb{V}$和$\pmb{W}$是两个$n$维向量,他们的点积为:
$$
\pmb{V}\pmb{W}=v_1w_1+···+v_nw_n
$$
点积又称内积或数量积
具有对称性、线性性、正定性
向量的膜
定义为
$$
||\pmb{V}||=\sqrt{V·V}=\sqrt{v_1^2+···+v_n^2}
$$
当$||\pmb{V}||=1$时,被称作单位向量
单位化:对于任意非零向量,$\frac{\pmb{V}}{||\pmb{V}||}$表示$V$方向上的单位向量
向量的夹角
$$
cos\theta=\frac{\pmb{V}·\pmb{W}}{||\pmb{V}||||\pmb{W}||}
$$
若$V·W>0$,则$cos\theta >0,0<\theta<\frac{\pi}{2}$
若$V·W<0$,则$cos \theta <0,\frac{\pi}{2}<\theta<\pi$
若$V·W=0$,则称两向量垂直或正交,记作$V\perp W$
规定零向量与任意向量垂直
两个不等式
1.Cauchy-Schwarz不等式:
$$|v·w|\leq ||v||||w||$$
当且仅当一个向量是另一个向量的倍数时等号成立
2.三角不等式:
$$|v+w|\leq ||v||+||w||$$
当且仅当一个向量是另一个向量的非负倍数时等号成立
矩阵(matrix)
$$A_{m\times n}=\begin{pmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{ij} & a_{23}\\
a_{31} & a_{32} & a_{mn}\\
\end{pmatrix},a_{ij}表示第i行第j列
$$
矩阵是一张 $m$ 行 $n$ 列的数表,用$a_{ij}$表示第$i$行第j列
- 用列向量表示:
$$
A=(\alpha_1,\alpha_2,\alpha_3···)
$$
方阵:行数和列数相等,有主对角线和副对角线
对角阵(diag):除对角线外的元素都为0的方阵
矩阵相等
- 行列数相同
- 对应元素相等
零矩阵
元素全是 $0$ 的矩阵
不同行列数的零矩阵不相等
矩阵与线性方程组
矩阵可由描述线性方程组而来,或由行列式而来
对矩阵与向量乘积的理解
$$
A\vec{x}
$$
- 理解1:得到$A$各列向量的一个线性组合
$$
A\vec{x}=(\mathbf{u},\mathbf{v},\mathbf{w})\begin{pmatrix}
x_{1} \\
x_{2} \\
x_{3} \\
\end{pmatrix}=x_{1}\mathbf{u}+x_{2}\mathbf{v}+x_{3}\mathbf{w}
$$
- 理解2:$A$各行向量与列向量$\vec{x}$做内积
$$
A \mathbf{x}=\left(\begin{array}{l}
\left(a_{11}, a_{12}, a_{13}\right) \cdot\left(x_1, x_2, x_3\right) \
\left(a_{21}, a_{22}, a_{23}\right) \cdot\left(x_1, x_2, x_3\right) \
\left(a_{31}, a_{32}, a_{33}\right) \cdot\left(x_1, x_2, x_3\right)
\end{array}\right)
$$
- 理解3:分块矩阵
对线性方程组的理解
$$
A\vec{x}=\vec{b}
$$
- 理解1:求$A$列向量的线性组合, 使之等于$\vec{b}$
- 理解2:求向量 $\vec{x}$, 使之与$A$的行向量内积分别为$\vec{b}$中的元素
可逆矩阵
若$A\vec{x}=\vec{b}$对任意向量$\vec{b}$有唯一解, 则称方阵$A$可逆,此时$\vec{x}=A^{-1}\vec{b}$($\vec{x}$ 可表示为 $A$ 的列向量的线性组合)
若$A=(\vec u, \vec v, \vec w)$可逆, 则$\vec u, \vec v, \vec w$的全部线性组合所得空间是整个三维空间, 这时向量$\vec u, \vec v, \vec w$线性无关/不共面, 相应$A \vec x=\vec b$只有零解
若矩阵的零解可以写成多种线性组合,这种情况称$A=(\vec u, \vec v, \vec w)$是奇异的(singular),向量$\vec u, \vec v, \vec w$是线性相关的
- 若方阵$A$的列向量线性无关,则$A$可逆,$A\vec{x}=0$只有零解
- 若方阵$A$的列向量线性相关,则$A$奇异,$A\vec{x}=0$有无穷多解
线性方程组的行图和列图
方程组$A_{m\times n}\vec{x}=\vec{b}$
每一行代表一个直线(n=2),或一个平面(n=3),或一个超平面(n>3)
- 此时解方程组$\Leftrightarrow$找行图的交点;
列的角度:解方程组求$\Leftrightarrow$求$\vec{b}$关于系数矩阵列向量$(\vec{\alpha_1,\alpha_2,\alpha_3…})$(不共线)的线性组合,若有唯一解则称矩阵是可逆的
Gauss消元法
步骤
- 通过交换方程和倍数相加得到阶梯矩阵,确定主元
- n个方程有n个主元$\Leftrightarrow$方程组有唯一解
- 消元终止$\Rightarrow$方程组无解或有无穷多解
结果
- 无解($0=c$)
- 有唯一解
- 无穷多解($0=0$)
矩阵表示
- $A\vec{x}=\vec{b}$表示线性方程组
- 单位矩阵:与任何向量相乘等于自身,$I\vec{b}=\vec{b}$
- 消去矩阵:将单位阵中某个$0$变为非零的数得到的矩阵,是一类初等矩阵
- 消元=消去矩阵同时左乘系数矩阵$A$和常数项$\vec{b}$
- 置换阵:将单位矩阵的第$i,j$行交换得到的矩阵,是一类初等矩阵
初等行变换和初等矩阵
方程组$A\vec{x}=\vec{b}$三种通解变形
- 把一个方程减去另一个方程的倍数
- 交换两个方程
- 用一个非零数乘一个方程
相应增广矩阵$(A|\vec b)$的三种行变换
- 把一行减去另一行的倍数
- 交换两行
- 用一个非零数乘一行
由单位矩阵经过一次行变换的矩阵成为初等矩阵
左乘换行,右乘换列;

矩阵的运算
加法
当两个矩阵行列数相等时才可以相加
$$
A+B:=(a_{ij}+b_{ij})_{m\times n}
$$
矩阵的加法满足:
交换律:$A+B=B+A$结合律$(A+B)+C=A+(B+C)$存在
零元:$A+0=A$存在
负矩阵:$A+(-A)=0$ (减法)
数乘
$$cA:=(ca_{ij})_{m\times n}$$
乘法

- 要求 : $A的列数=B的行数$
$$
A_{m\times s}B_{s\times n}=C_{m\times n}
$$
$$
C_{ij}=a_{i1}b_{1i}+a_{i2}b_{2i}+···+a_{in}b_{mi}
=\sum_{k=1}^n a_{ik}b_{kj}
$$
${\displaystyle c_{ij}}$是$A$的第$i$行和$B$的第$j$列的点积
$$
AB的第i行=(A的第i行)B
$$
结合律:$(AB)C=A(BC)$左分配律$A(B+C)=AB+AC$右分配律$(B+C)A=BA+CB$- $k(AB)=(kA)B=A(kB),k为任意常数$
- $I_mA=A=Ai_n$
- $AB\neq BA$(不一定相等)
- 若$AB=BA$,则称$A$和$B$是可交换的
- 不满足
消去律
左乘
设矩阵$B$的列向量是$b_1,b_2,···,b_p$,借助矩阵和向量乘积的定义:
$$
AB=A(\vec b_1,\vec b_2,···,\vec b_p):=(A\vec b_1,A\vec b_2,···,A\vec b_p)
$$
矩阵的每一列$A\vec b_i$是矩阵$A$的行向量的线性组合
右乘
$$
AB=\begin{pmatrix}
\vec \alpha_{1} \\
\vec \alpha_{2} \\
\vec \alpha_{3} \\
\end{pmatrix}B=\begin{pmatrix}
\vec \alpha_{1}B \\
\vec \alpha_{2}B \\
\vec \alpha_{3}B \\
\end{pmatrix}
$$
矩阵的每一行$\vec \alpha_{i}B$是矩阵$B$的列向量的线性组合
方幂
只有方阵可以有幂运算。
$$
A^n=\underbrace{A···A}_n
$$
$A^0=I_n$
$A^p·A^q=A^{p+q}$
$(A^{p})^q=A^{pq}$
因为$AB\neq BA$,所以:
- $(A + B)^2\neq A^2+ 2AB+B^2$
- $(A+B)(A-B)\neq A^2-B^2$
分块矩阵
用于大型矩阵运算,运算法则与矩阵相同
$$
A=\left(
\begin{array}{c|cc}
A_{11} & A_{12} \\
\hline
A_{21} & A_{22} \\
\end{array}
\right)
$$
初等块行变换:(列变换为右乘)
- 一个块行
减去另一个块行左乘$P$ - 两个块行
互换位置 - 用一个可逆矩阵
左乘某一块行
转置
将$A_{m\times n}$行列互换成$A_{n\times m}$,得到转置矩阵$A^T$,与原来矩阵$A$成对角线对称。
- $(A^T)^T=A$
- $(A+B)^T=A^T+B^T$
- $(kA)^T=kA^T$
- $(AB)^T=B^TA^T $
由4,有:$(A_1···A_k)^T=A_k^T···A_1^T$
若$A^T=A$ , $A$ 为对称矩阵
若$A^T=-A$,$A$为反对称矩阵
- 设$R_{m\times n}$,则$RR^T$ 为 $m\times m$的对称阵,$R^TR$ 为 $n\times n$的反对称阵,其对角元非负,两个矩阵的元的和(trace)相等。
转置的应用
例: 向量内积:$\mathbf{x·y=x^T y=y^T x}$
可逆矩阵
类似$a\times \frac{1}{a}=1$,在矩阵中称 $\frac{1}{a}$ 为逆
若 $AB=BA=I$,则称 矩阵$A$ 是可逆的,$B$为$A$的逆矩阵,记作$A^{-1}$.
不可逆矩阵可以称为奇异矩阵,例如零矩阵;
可逆矩阵可以称为非奇异矩阵
- 若方阵 $A$满足$AB=I,CA=I$,则$B=C$,特别的,方阵的逆唯一.
- $A可逆\Leftrightarrow A\vec{x}=\vec{b}有唯一解\vec{x}=A^{-1}\vec{b}$
- $A\vec{x}=0有非零解 \Leftrightarrow A不可逆$
- 对角矩阵的逆为对角矩阵元的倒数
- 二阶方阵的逆:
$$A_{2\times 2}=\left(
\begin{array}{cc}
a & b \\
c & d \\
\end{array}
\right)可逆\Leftrightarrow ad-bc\neq 0,且A^{-1}=\frac{1}{ad-bc}\left(
\begin{array}{cc}
d & -b \\
-c & a \\
\end{array}
\right)
$$
- $(A^{-1})^{-1}=A$,$A$可逆则$A^{-1}$也可逆
- $(AB)^{-1}=B^{-1}A^{-1}$,$n$阶方阵$A$和$B$都可逆,则$AB$可逆
- $(A^{T})^{-1}=(A^{-1})^T$,$A$可逆则$A^{T}$也可逆
初等矩阵的逆
初等矩阵都是可逆的,它的逆是将其变回单位矩阵的初等矩阵。
例子:$E_{21}(-5)E_{21}(5)=I$
Gauss-Jordan消元法
若A是可逆的,将分块矩阵 $(A|I)$ 通过初等变换,可得到 $(I|A^{-1})$
扩展:求解$A\bold{x}=B$,可以求$(A|B)\rightarrow (I|A^{-1}B)$,$\bold{x}=A^{-1}B$
推论:
$$A可逆\Leftrightarrow A可表示成一系列初等矩阵的乘积$$
$$n阶方阵A可逆\Leftrightarrow A有n个主元$$
三角阵的逆
两个 $n$ 阶下(上)三角矩阵 $A$ 与 $B$ 的乘积仍为下(上)三角矩阵
且 $AB$ 的主对角元等于 $A$ 与 $B$ 的相应主对角元的乘积.
可逆下三角矩阵的逆也是下三角阵
分块上三角矩阵可逆$\Leftrightarrow$主对角线上各分块都是可逆的
伴随矩阵
A的伴随矩阵是一个n×n的矩阵,使得其第i 行第j 列的元素是A关于第j行第i列的代数余子式
$$
[adj(A)]{ij}=C{ij}
$$
Cramer’s rule
$$
设(\alpha _1,\alpha _2,\alpha _3,\beta) \Leftrightarrow Ax=B\\
A=(\alpha _1,\alpha _2,\alpha _3)\\
A_i=(\beta,\alpha _2,\alpha _3)(i=1)
$$
$$
则x=\frac{det|A_x|}{det|A|},y=\frac{|A_y|}{|A|},z=\frac{|A_z|}{|A|}
$$
矩阵的秩
子式
对于$m\times n$的矩阵$A$,任取$k$行$k$列,不变次序得到的含有$k^2$个元素的矩阵,称为$A$的$k$阶子式
秩的行列式定义
$A_{m×n}$的不为零的子式的最大阶数称为矩阵A的秩,记作r(A),或rankA或R(A)
零矩阵的秩为0;
等价矩阵秩相同
$$
0\leq R(A) \leq min(m,n)
$$
参考资料
[1].《线性代数(第六版)》.同济大学.高等教育出版社
[2].《学堂在线:线性代数(1)》.马辉、徐帆